The Reference Frame: Why stringy enhanced symmetries are ...

A TRF reader expressed the following sentiment:

I would have liked to see the gauge symmetries of standard model emerging purely from the 10-dim geometry.

In other words, he would have liked if string theory were nothing more than the Kaluza-Klein theory (general relativity with extra dimensions) from the 1920s. Well, the bad news for him is that string theory also contains... strings, for example, and they actually have physical consequences. It is not just Kaluza-Klein theory.

The quote above is just one example of the widespread prejudices and excuses by which people who don't like to learn new things about science try to justify their frozen closed minds.

The most generic group of those folks would say: "I would have liked string theory if it just said that everything is made out of five elements, earth, air, water, fire, and aether." A more sophisticated subgroup ? one that has already figured out that the world is more subtle than just five elements ? would have liked the current physics if it said that everything were just classical mechanics; or classical field theory; or non-relativistic quantum mechanics; or a simple quantum field theory, and so on.

But those folks are just stuck in various points of the history of science. They are trying to squeeze Nature and science into assorted straitjackets. They are claiming that their ideas are beautiful and convincing; in reality, they are obsolete and demonstrably wrong.

Different people from those groups want to be frozen at different points of the history.

But I want to return to the particular topic introduced by the quote above: the emergence of gauge symmetries in string theory. String theory is a theory of everything so the gauge symmetries are not "assumptions we have to insert" which is the status of gauge symmetries in quantum field theories (at least if we "construct them" in the beautified ways).

In string theory, gauge symmetries, much like everything else, emerge from a more fundamental substrate. And the emergence of these gauge symmetries depends on several very original "tricks" that Nature and mathematics knew from their birth but humans had to gradually learn them. Let me start with the faces of gauge symmetries that string theory shares with previous frameworks of physics.

Pre-history 1: Chan-Paton factors

In quantum field theory, fields like the quark fields carry various color indices and similar indices, \(\psi_i\), \(i=1,2,3\). If you realize that these fields may create particles (or annihilate their antiparticles), the index literally means that there are point-like particles called quarks with three different colors. You may visualize them as red, green, blue points although the actual quantum number known as "color" has fundamentally nothing to do with the "colors" associated with various wavelengths of visible light, of course.

For many decades, people have realized that there exist objects that carry the same "colors" or discrete indices as the index \(i\) of the quark above. It's because string theory has been known to contain point-like-particle-like objects, namely the endpoints of the open strings.

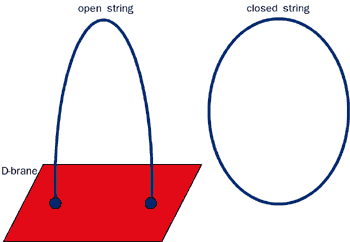
An open string is on the left side, a closed string is on the right side.

Note that one may ban open strings in a string theory; but one may never ban closed strings. Why? To make open strings dynamical, we must allow them to break and join and change the number of endpoints by 2; otherwise such open strings would be indestructible but nothing in the world is indestructible. However, once we allow two open strings to merge their endpoints, the same local interaction is also capable of merging the endpoints of a single open string, thus creating a closed one. The endpoints can't know whom they belong to, by locality, so it is always possible to produce closed strings by string interactions. It's good news because the gravitational field is always carried by closed strings ? so gravity is always a part of string theory.

On the other hand, string theory may "ban" all open strings. In type II string theory, the open strings exist if there are D-branes around. In heterotic string theory, there can't be open strings at all.

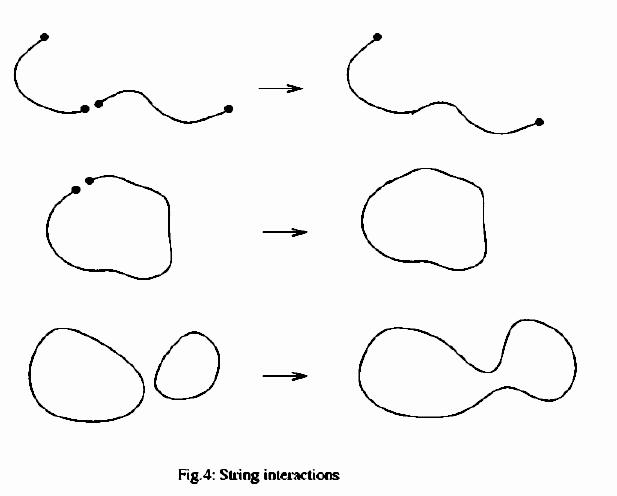
If we allow open-string-merging interactions at the top, we also allow open-to-closed interactions in the middle because they're locally the same processes. On the other hand, there can be string theories with closed string only. The bottom part of the diagram is the only allowed "crossover-type" interaction in these theories.

But let me return to the colorful quarks. The open strings' endpoints look like quarks or antiquarks so they may also be marked by colors; they may carry additional discrete information about the color, an index. If an open string is orientable, we may invariantly distinguish its beginning, the beginning of the arrow, and its end, the end of the arrow. We may call the former and the latter "quark" and "antiquark", respectively. The open string field creating such an open string therefore carries two color indices, one from a quark and one from an antiquark,\[

\Psi_i^j.

\] You see that because of the two indices of the opposite type, the open strings transform as the adjoint representation of a \(U(N)\) group. That's for the same reason as the reason why the quarks in QCD ? which have a single index ? transform in the fundamental representation (and antiquarks in the antifundamental representation).

The open-string-splitting-or-joining interaction annihilates a quark and antiquark of the same color only; or it creates them in a color-blind way. At any rate, the interactions between such open strings are proportional to \(\delta_i^j\). That's why the spectrum as well as the interactions are automatically invariant under the \(U(N)\) symmetry transformations

In fact, it's straightforward to see that this \(U(N)\) is actually a gauge symmetry in the spacetime. Much like closed strings inevitably contain a massless mode, the graviton, the open strings inevitably contain a massless mode, the gauge boson. If the open strings have the minimal (or next-to-minimal, in theories with tachyons) amount of internal vibrational energy, the field \(\Psi_i^j\) actually carries an extra Lorentz index \(\mu\) and it creates or annihilates a gauge boson of a \(U(N)\) gauge symmetry. One may show that this symmetry is local in spacetime or, equivalently, the time-like and longitudinal polarizations of the gauge field decouple. The latter property boils down to the conformal symmetry on the world sheet ? which is a "more elementary" reason that produces gauge symmetries as well as the diffeomorphism symmetry of general relativity and many other things we know from the spacetime. But I won't offer you the proof here.

If strings are unorientable (if that holds for closed strings, it must hold for open strings and vice versa because the bulk of the strings is always the same and you must know whether it carries a preferred arrow or not without asking whether the string ends up as an open one or a closed one), you can't distinguish the beginning and the end. Consequently, the endpoints are quarks and antiquarks at the same moment. The projection needed to identify the oppositely oriented strings has the effect of reducing the \(U(N)\) symmetry either to \(O(N)\) or \(USp(N)=USp(2k)\); the unitary group gets reduced to the orthogonal one or the symplectic one. Note that the orthogonal and symplectic groups don't distinguish the fundamental and the anti-fundamental representation, unlike the unitary groups. That's why the corresponding strings are unorientable.

So when we have open strings, we may make them either orientable or not and we may assign their endpoints with labels that distinguish colors. The number of colors is a priori variable. For bosonic string theory, there is no number of colors that would yield a more consistent or interesting theory than other numbers of colors. Well, that's not quite the case as Steven Weinberg has explained why the open bosonic string theory with the \(SO(8192)\) gauge group cancels some tadpoles and one-loop divergences.

For the superstring theory, the choice of the right number of colors is much more important. In 1984, Green and Schwarz realized that almost all choices led to anomalous theories but the unorientable \(SO(32)\) open "type I" strings miraculously cancel all world sheet and spacetime anomalies. Quite unexpectedly, a half-dozen of coefficients which are a priori integers comparable to a thousand get cancelled due to contributions from a half-dozen of sources. All of them vanish at the end! This miracle had sparked the first superstring revolution in the mid 1980s.

If you think about Weinberg's \(SO(8192)\) gauge group in an IQ-test-style way, you might figure out that the superstrings' preferred gauge group is \(SO(32)\). How? Well, \(8192=2^{13}\) and \(13\) is not only an unlucky number but also one-half of \(D=26\) which is the critical spacetime dimension of bosonic string theory. If you repeat the same exercise with the \(D=10\) critical dimension of the superstring, divide it by two, obtain five, and calculate the fifth power of two, you get \(SO(32)\). This is not a coincidence but a genuine caricature of the calculation of the preferred gauge group.

In type I string theory, the Green-Schwarz-sponsored \(SO(32)\) group arises from colored endpoints of the open strings. In some sense, the colorful labels are added in the same ad hoc way as they are in quantum field theories. In the context of open strings, we call these colorful labels "Chan-Paton factors".

This article will be completed and proofread later, hopefully not later than tomorrow.

Pre-history 2: Old-fashioned Kaluza-Klein theory

String theory's added value 1: \(p\)-forms

String theory's added value 2: enhanced non-Abelian symmetries at self-dual radii and abstract CFTs with current algebras

The heterotic case

Chan-Paton factors in the D-brane language

String theory's added value 3: groups from ADE-like singularities

String theory's added value 4: boundaries of M-theoretical worlds

Source: http://motls.blogspot.com/2012/08/why-stringy-enhanced-symmetries-are.html

2012 senior bowl chuck series finale welcome back kotter 2001 a space odyssey barefoot bandit polar bear plunge lovelace